집합(Set).
기초 수학에서 집합은 (특정조건에 맞는)원소들의 모임을 의미합니다.
집합은 중복되지 않는 원소들로 구성되며, 순서는 중요하지 않습니다.
집합은 중괄호{}로 표현되며, 각 원소는 쉼표로 구분됩니다.
집합을 표현하는 방법으로는 원소나열법, 조건제시법, 벤 다이어그램이 있습니다.
집합에 대해 알아보며 이를 자바 코드로 구현해봅시다.
집합 표현 방법.
- 원소나열법
A = {1, 2, 3, 4, 5}, B = {2, 4, 6, 8, 10}- 조건제시법
A = {A | A는 정수, 1 ≦ A ≦ 5 }
B = {2B | B는 정수, 1 ≦ B ≦ 5}- 벤 다이어그램

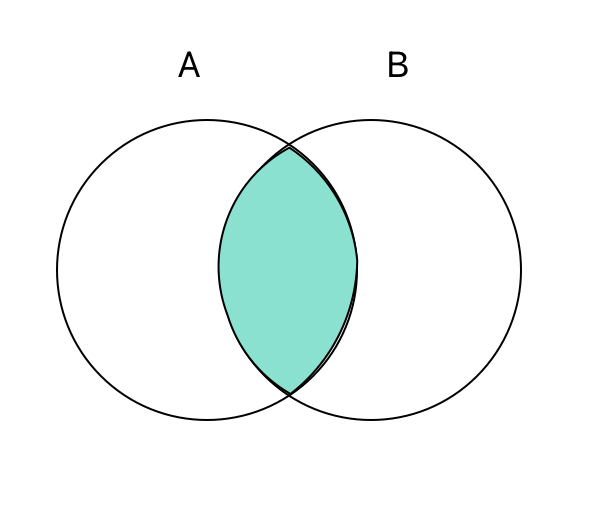
교집합.
두 집합이 공통으로 포함하는 원소로 이루어진 집합
A ∩ B = { 𝑥 | 𝑥 ∈ A and 𝑥 ∈ B }
합집합.
어느 하나에라도 포함되는 원소들을 모두 모은 집합
A ∪ B = { 𝑥 | 𝑥 ∈ A or 𝑥 ∈ B }

차집합.
A (또는 B)에만 속하는 원소들의 집합
A − B = { 𝑥 | 𝑥 ∈ A and 𝑥 ∉ B }

여집합.
전체집합(U) 중 A의 원소가 아닌 것들의 집합

자바에서 사용하는 HashSet 메서드.
package day028;
import java.util.Arrays;
import java.util.HashSet;
public class MathSetTest {
public static void main(String[] args) {
HashSet<Integer> set = new HashSet<>();
// 데이터 추가 - 중복값 추가하지 않음
set.add(1);
set.add(1);
set.add(2);
set.add(3);
System.out.println(set); // [1, 2, 3]
// 크기
System.out.println(set.size()); // 3
// 삭제
set.remove(1);
System.out.println(set); // [2, 3]
// 집합 A, 집합B
HashSet<Integer> a = new HashSet<>(Arrays.asList(1, 2, 3, 4, 5));
HashSet<Integer> b = new HashSet<>(Arrays.asList(2, 4, 6, 8, 10));
// 교집합
a.retainAll(b);
System.out.println(a); // [2, 4]
// 합집합
a.addAll(b);
System.out.println(a); // [2, 4, 6, 8, 10]
// 차집합
a.removeAll(b);
System.out.println(a); // []
}
}
ArrayList로 Set 만들기.
package day028;
import java.util.ArrayList;
class MySet {
ArrayList<Integer> list;
MySet() {
this.list = new ArrayList<>();
}
MySet(int[] arr) {
this.list = new ArrayList<>();
for(int n : arr) {
this.list.add(n);
}
}
// add 구현하기, 중복 X
public void add(int x) {
for (int item : this.list) {
if (item == x) {
return;
}
}
this.list.add(x);
}
// 교집합 구현
public MySet retainAll(MySet b) {
MySet result = new MySet();
for (int item : this.list) {
for (int itemB : b.list) {
if (item == itemB) {
result.add(item);
}
}
}
return result;
}
// 합집합 구현
public MySet addAll(MySet b) {
MySet result = new MySet();
for (int item : this.list) {
result.add(item);
}
for (int item : b.list) {
result.add(item);
}
return result;
}
// 차집합
public MySet removeAll(MySet b) {
MySet result = new MySet();
for (int item : this.list) {
boolean retainFlag = false;
for (int itemB : b.list) {
if (item == itemB) { // a 의 원소와 b의 원소가 같다면
retainFlag = true; // 트루로 변경하고
break; // 멈춤
}
}
if (!retainFlag) { // false면
result.add(item); // a에 남는 원소가 되니까 결과에 add 반복
}
}
return result;
}
}
public class MathMySetTest {
public static void main(String[] args) {
MySet a = new MySet();
a.add(1);
a.add(1);
a.add(2);
a.add(3);
System.out.println(a.list); // [1, 2, 3]
a = new MySet(new int[] {1, 2, 3, 4, 5});
MySet b = new MySet(new int[] {2, 4, 6, 8, 10});
MySet result = a.retainAll(b);
System.out.println(result.list); // [2, 4]
result = a.addAll(b);
System.out.println(result.list); // [1, 2, 3, 4, 5, 6, 8, 10]
result = a.removeAll(b);
System.out.println(result.list); // [1, 3, 5]
}
}
'BACKEND > Data Structure & Algorithm' 카테고리의 다른 글
| 기초수학 - 순열(Permutation) (0) | 2023.06.03 |
|---|---|
| 기초수학 - 경우의 수 : 합의법칙, 곱의법칙, 약수, 최대공약수, 최소공배수) (0) | 2023.06.01 |
| 비선형 자료구조 - 이진 탐색 트리 (Binary Search Tree) 정의 및 탐색, 삽입, 삭제 구현 (0) | 2023.05.29 |
| 비선형 자료구조 - 이진 트리(Binary Tree) 구현과 순회 (0) | 2023.05.27 |
| 비선형 자료구조 - 이진 트리(Binary Tree)란 무엇이고 여러 가지 종류를 알아보자 (0) | 2023.05.27 |